现况

现有的滤波器剪枝的标准是，“smaller-norm-less-important”，即认为滤波器的范数（p-norm）越小，相对应的特征图越接近于 0，于是对网络对贡献越小，那么这些滤波器可以去掉而不会严重影响网络的性能。但作者认为这个标准要达到好的效果需要满足两个前提：

不同卷积核之间的范数差距要够大
最不重要的（范数最小的）卷积核的范数要够小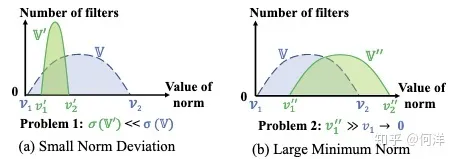即如图 (a) 可能会导致卷积核之间的重要性难以区分，间隔区间太小，而图 (b) 剪去的卷积核的范数还是很大，即对结果的影响还是很大，删去后影响较大。

介绍

因此，作者提出了一种用几何中位数来描述卷积核的可替代性，从而进行剪枝的方案

几何中位数是对于欧几里得空间的点的中心的一个估计。我们认为滤波器也是欧氏空间中的点，于是我们可以根据计算 GM 来得到这些滤波器的“中心”，也就是他们的共同性质。如果某个滤波器接近于这个 GM，可以认为这个滤波器的信息跟其他滤波器重合，甚至是冗余的，于是我们可以去掉这个滤波器而不对网络产生大的影响。去掉它后，它的功能可以被其他滤波器代替。

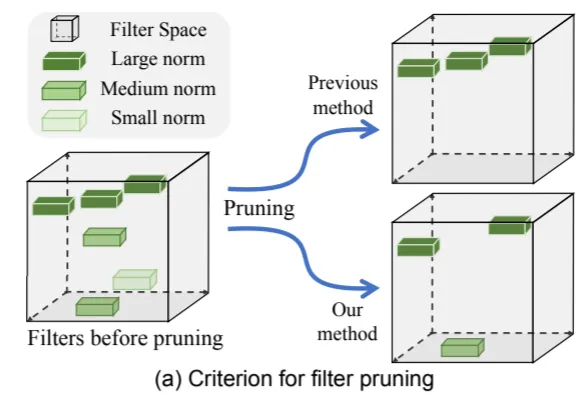右上角即为传统方法进行剪枝，右下角为作者提出的方法（FPGM)进行剪枝和之前看的 [[Network Compression Based on Filter Similarity Pruning for Fast Inference on Edge Devices.pdf | 根据卷积核相似性进行剪枝]] 类似，都是考察卷积核的可替代性，可以用其他的卷积核包含的信息来替代某个卷积核，那么该卷积核即可被删去且对结果影响寥寥。

欧式距离即两点之间的距离== 在两篇论文中，欧式距离都被用来进行计算并作为相关依据，该论文计算在欧式空间中的中位值来选择可被替代剪枝的卷积核，在根据卷积核相似性剪枝的论文中，通过计算每个卷积核之间的欧式距离，来作为衡量两者相似性的依据

主要贡献：

分析了之前的基于范数的剪枝规则，说明了其限制条件
提出了基于几何中位数进行剪枝的方法 FPGM
通过实验证明了 FPGM 的有效性

公式

首先，假设给定 n 个点 $a^{(1)},…,a^{(n)}$，$\forall a^{(i)} \in \mathbb{R}^d$，找到一个点 $x^$ 使得与所有其他点的欧氏距离之和最小$$x^ \in \mathop{argmin}{x \in \mathbb{R}^d}f(x)\quad where\quad f(x) \mathop=^{def} \sum{i \in [i,n]} ||x-a^{(i)}||_2 \tag{1}$$

argmin 指使后面这个式子达到最小值时的 x 的取值 $||x||_2$ 表示 x 的范数，实际就是模长的开根号，|x|表示模长，||x||表示在外套个绝对值设$x=<x_1,x_2,x_3>$，则$||x||_2 = \sqrt{x_1^2 + x_2^2 + x_3^2}$ $\mathbb{R}^d$表示都是x都是d维的

接下来定义 $F_i^{GM}$ 为卷积核的第 $i$ 层的几何中位数，GM 指 Geometry Median - 几何中位数，$N_i$ 表示第 $i$ 层，也可表示输入维度，$N_{i+1}$ 表示第 $i+1$ 层，也表示输出维度 $$F_i^{GM}\in\mathop{argmin}{x \in\mathbb{R}^{N_i \times K \times K}}g(x) \tag{2}$$ 其中 $$g(x)\mathop{=}^{def}\sum{j’\in[1,N_{i+1}]}||x-F_{i,j’}||2 \tag{3}$$ 这里将 $x$ 点换成了卷积核，卷积核有 $N_i$ 个，每个大小为 $K \times K$ ，2、3 式即表示卷积核的几何中位数（ $F_i^{GM}$ ）为使得到该 $i$ 层每个卷积核的欧氏距离之和最小的一个值。然后在第 $i$ 层中，找到离该几何中位数最接近的一个卷积核，将其删去，设为 $F{i,j^}$ 则 $$F_{i,j^}\in\mathop{argmin}{j’\in[1,N{i+1}]}||F_{i,j’}-F_i^{GM}||_2 \tag{4}$$

在接下来，作者做了一个简化，即”假设所有剪去的卷积核都在几何中心“，也就是 $$||F_{i,j^}-F_i^{GM}||2 = 0 \tag{5}$$ 这样的话也就是 $F{i,j^}==F_i^{GM}$，那么找到每个距离几何中位数最近的卷积核，就可以转成计算每个位于几何中心的卷积核，也就是这些卷积核全部满足（2）式的要求，即$$F_{i,j^}\in\mathop{argmin}_{j^\in[1,N_{i+1}]}g(x) \tag{6}$$

伪代码

实现代码

def get_filter_similar(self, weight_torch, compress_rate, distance_rate, length):
    codebook = np.ones(length)
    if len(weight_torch.size()) == 4:
        filter_pruned_num = int(weight_torch.size()[0] * (1 - compress_rate))
        similar_pruned_num = int(weight_torch.size()[0] * distance_rate)
        weight_vec = weight_torch.view(weight_torch.size()[0], -1)
        # norm1 = torch.norm(weight_vec, 1, 1)
        # norm1_np = norm1.cpu().numpy()
        norm2 = torch.norm(weight_vec, 2, 1)
        norm2_np = norm2.cpu().numpy()
        filter_small_index = []
        filter_large_index = []
        filter_large_index = norm2_np.argsort()[filter_pruned_num:]
        filter_small_index = norm2_np.argsort()[:filter_pruned_num]

        # distance using numpy function
        indices = torch.LongTensor(filter_large_index).cuda()
        weight_vec_after_norm = torch.index_select(weight_vec, 0, indices).cpu().numpy()
        # for euclidean distance
        similar_matrix = distance.cdist(weight_vec_after_norm, weight_vec_after_norm, 'euclidean')
        # for cos similarity
        # similar_matrix = 1 - distance.cdist(weight_vec_after_norm, weight_vec_after_norm, 'cosine')
        similar_sum = np.sum(np.abs(similar_matrix), axis=0)

        # for distance similar: get the filter index with largest similarity == small distance
        similar_large_index = similar_sum.argsort()[similar_pruned_num:]
        similar_small_index = similar_sum.argsort()[:  similar_pruned_num]
        similar_index_for_filter = [filter_large_index[i] for i in similar_small_index]

        kernel_length = weight_torch.size()[1] * weight_torch.size()[2] * weight_torch.size()[3]
        for x in range(0, len(similar_index_for_filter)):
            codebook[
                similar_index_for_filter[x] * kernel_length: (similar_index_for_filter[x] + 1) * kernel_length] = 0
            print("similar index done")
            else:
                pass
            return codebook