定点数

定点数的格式（小数点位置固定不变）

1. 定点整数（小数点约定在最低位的右边，最高位为符号位）

   Xn-1	Xn-2	…	X0	. —(小数点在最低位右侧)

2. 定点小数（最高位为符号位，小数点约定在符号位右侧）

   Xn-1	. —(小数点在符号位右侧)	Xn-2	…	X0

定点数的表示范围

1. 无符号定点整数：0 $\le$ X $\le$ 2^n^-1
2. 有符号定点整数（补码）：-2^n-1^ $\le$ X$\le$ 2^n-1^-1
3. 有符号定点小数（补码）：-1 $\le$ X $\le$ 1-2^-n+1^

定点整数的真值是定点小数的真值的2^n+1^倍

浮点数

定点数与浮点数的比较：

• 定点数表示数的范围比较小，运算容易发生溢出
• 浮点数表示数的范围比较大，运算不容易发生溢出

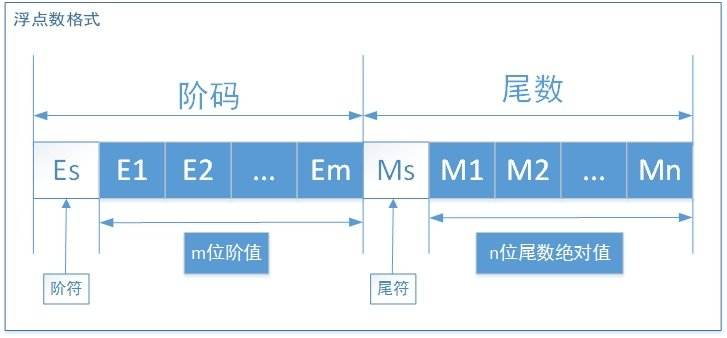
浮点数格式： 尾数决定了数的精度，阶码决定了数的范围。 其中Es为阶符，即从这开始到尾符之间是阶码 Ms为尾符，表明尾数部分从此开始。

浮点数的规格化表示

浮点数的规格化形式

• M>0（正数形式）：0.1xx…，即$\frac{1}{2}\le M\le$ 1-2^-n+1^
• M<0（负数形式）：1.0xx…，即-1 $\le M \le -\frac{1}{2}-$ 2^-n+1^

（-1/2）补 = 1.100…0

规格化浮点数 尾数进行移位，阶码做相应加减运算，直至尾数满足要求（类比科学记数法）

• 左规：尾数每左移一次，阶码相应减1
• 右规：尾数每右移一次，阶码相应加1

规格化的意义

• 使机器真值的表示形式唯一
• 充分利用尾数更多的有效数字

✨规格化浮点数的表数范围 设阶码：p位（含阶符），移码；尾数：m位（含尾符），补码

• 最大正数：0.11…1$×$ 2^11…1^ $$(1-2^{-m+1})·2^{(2^{p-1}-1)}$$
• 最小正数：0.10…0$×$ 2^00…0^ $$\frac{1}{2}·2^{-2^{p-1}}$$
• 最大负数：1.01…1$×$ 2^00…0^ $$-(\frac{1}{2}+2^{-m+1})·2^{-2^{p-1}}$$
• 最小负数：1.00…0$×$ 2^11…1^ $$-2^{(2^{p-1}-1)}$$

浮点数既可以表示数值范围很大的数，也可以表示数值范围很小但精确度很高的数

• 阶码的位数（p），决定表示数的范围
• 尾数的位数（m），决定表示数的精度

浮点数的溢出判断 在最大负数和最小正数之间的称为下溢区 大于最大正数以及小于最小负数的区域称为上溢区

溢出判断只是对规格化数的 ==阶码== 进行判断

• 下溢：自动视为0
• 上溢：溢出处理