动态规划的中的最长公共子序列示例题。
示例
题目
设计一个O(n^2^)时间的算法,找出由n个数组成的序列的最长单调递增子序列。
简要分析
题目可以看做原序列和排序后序列求最长公共子序列。
基础
一个给定序列的子序列是在该序列中删去若干元素后得到的序列。
设给定序列X={x1,x2,x3,…xm},若存在子序列Z={z1,z2,z3,….,zk},那么,
必定存在一个严格递增的下标序列{i1,i2,i3,….ik},使得所有j=1,2,3,…,k,都有zj=xij
例如:
X={A,B,C,B,D,B,A},则其子序列Z={B,C,D,A},相应的下标序列为{2,3,5,7}(下标从1开始)
此时,当j=1时,z1=B,x的下标为i1,即xi1,i1也就是下标序列中的第一位,即2,
所以,z1=x2=B,同理,当j=4时,z4=xi4=x7=A
当给定两个序列X和Y,且Z同时为两者的子序列时,则称Z为X和Y的公共子序列
例如:
X={A,B,C,B,D,B,A},Y={B,D,C,A,B,A}
若Z={B,C,A},则Z是X,Y的公共子序列
若Z={B,C,B,A},则Z是X,Y的公共子序列,同时也是最长公共子序列
计算最长公共子序列
设序列X={x1,x2,x3,…xm},和序列Y={y1,y2,y3,….,yn}的最长公共子序列为Z={z1,z2,z3,….,zk},则有三种情况
- 若xm=yn,则zk=xm=yn,且zk−1是Xm−1和Yn−1的最长公共子序列
- 若xm≠yn且zk≠xm,则Z是Xm−1和Yn的最长公共子序列
- 若xm≠yn且zk≠yn,则Z是Xm和Yn−1的最长公共子序列
①xm=yn,说明X和Y的最后一个元素相同,而Z是X和Y的最长公共子序列,而最长自然最好是从头到尾,既然两者的尾元素相同,那自然应该包含在最长公共子序列中,且应是最后一位。三者同时将最后一位去掉,即得到Zk−1是Xm−1和Yn−1的最长公共子序列
证:
若zk≠xm,则因为Z是X和Y的最长公共子序列,且xm=yn,则说明{Z,xm/yn}也应该是X和Y的公共子序列,因为Z的长度是k,而{Z,xm/yn}的长度为k+1,k+1>k,这与”Z是X和Y的最长公共子序列设定“冲突,所以必有zk=xm=yn,即当xm=yn时,xm/yn必定在最长子序列Z中。
②/③Z是X和Y的最长公共子序列,而zk是Z中的最后一位,xm是X中的最后一位,若zk≠xm,说明xm不包含于Z中,即Xm不是最长公共子序列的一部分,那么可以将其去掉,即最长公共子序列存在于和Xm−1和Yn中
分析递归结构
由上可知,当xm=yn时,找出和xm−1和yn−1的最长公共子序列,在气候加上xm,即是X和Y的最长公共子序列;当xm≠yn时,则分别求和Xm−1和Yn的最长公共子序列,以及和Xm和Yn−1的最长公共子序列,并比较得到较长的那个序列,即为X,Y的最长公共子序列。
用C[i][j]记录序列和Xi和Yj的最长公共子序列的长度。
例:
C[5][7]即是X5={x1,x2,….,x5}和Y7={y1,y2,….,y7}的最长公共子序列
当i=j=0时,说明X和Y都是空序列,那么最长公共子序列的长度也自然是0,得到公式
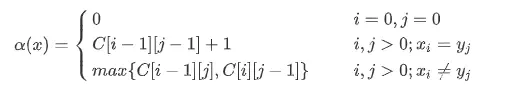
图表分析
另外设一个数组b[i][j]用来记录符合哪一种情况,即上述方式中的四种情况。
X=[5,2,3,4,8,6,9],Y为升序的X,Y=[2,3,4,5,6,8,9]
C表:
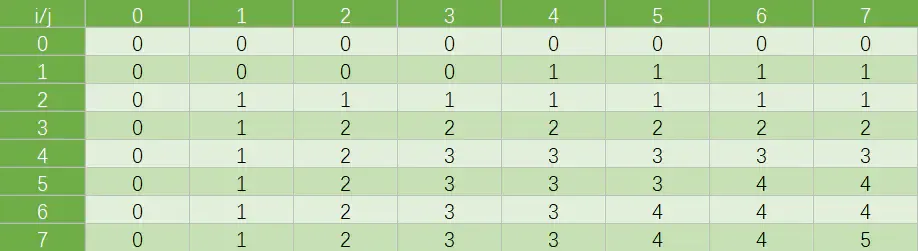
b表:(第一种情况用作边界条件,设上述第二种情况为1,第三种情况的左侧大为2,右侧大为3)
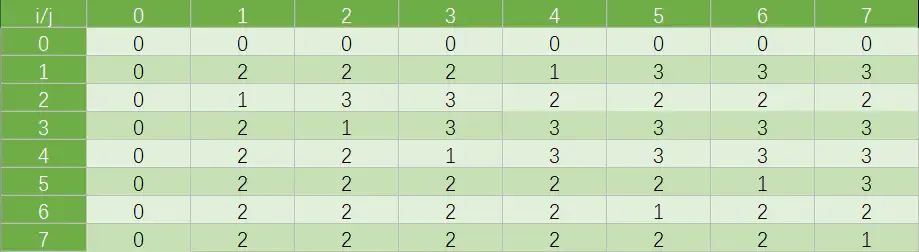
示例:
当i=1的时候,,x1≠y1,i,j≠0那么看第三种方案中的两种情况,C[i−1][j]=C[0][1]=0,C[i][j−1]=C[1][0]=0,这里将他归入”2“,即C[i−1][j]≥C[i][j−1],所以此时C[1][1]=C[i−1][j]=C[0][1]=0,为”2“情况,所以b[1][1]=2,依次类推,直到j=4时,x1=y4,此时满足第二种情况,所以C[1][4]=C[0][3]+1=1,b[1][4]=1
依次类推,当i=7,j=7时,返回C[7][7]即为最长子公共序列的长度,并返回b数组用于输出该最长子公共序列。
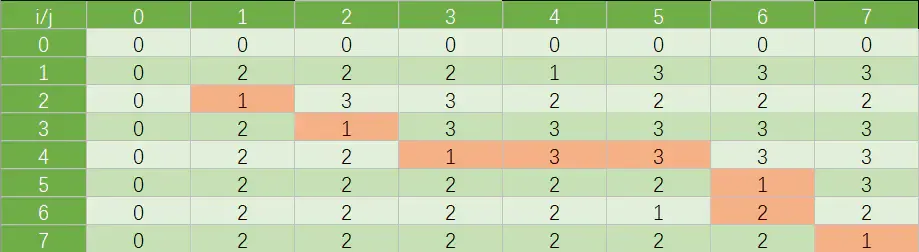
如上图所示,根据b数组进行查找输出。
首先b[7][7]=1,说明x7在最长公共子序列中可以输出,但应是最晚输出,因为是1,所以找C[6][6],即左上角,左上角为2,则说明该值由C[i−1][j]得来,找上方一格,即C[5][6],此时C[5][6]=1,说明该值在最长公共子序列中,即x5在最长公共子序列中,再找左上角,为3,找左边,为3,找左边,为1,说明可输出,找左上角。类推。
最终输出结果x2,x3,x4,x5,x7,即23489。
注意点
这里我们可以注意到除了23489之外,23469也可以,这点取决于当和C[i−1][j]和C[i][j−1]相等时取谁。
代码
public static int[] Sort(int[] arr) {
int length = arr.length;
for (int i = 0; i < arr.length; i++) {
//每一趟循环比较时,min用于存放较小元素的数组下标,
//这样当前批次比较完毕最终存放的就是此趟内最小的元素的下标,避免每次遇到较小元素都要进行交换。
int min = i;
for (int j = i + 1; j < arr.length; j++) {
if (arr[j] < arr[min]) {
min = j;
}
}
//进行交换,如果min发生变化,则进行交换
if (min != i) {
int temp = arr[i];
arr[i] = arr[min];
arr[min] = temp;
}
}
int i = 0;
//去重
while(i<length-1)
{
if(arr[i] == arr[i+1])
{
for(int j=i;j<length;j++)
{
arr[j]=arr[j+1];
}
length--;
}
else
i++;
}
int []b = new int[length];
for(int j=0;j<length;j++)
{
b[j] = arr[j];
}
return b;
}
/**
* 构建最长公共子序列
* @param i x序列的下标?
* @param j y序列的下标?
* @param x 序列x
* @param b 通过lcsLength()得到的状态数组?
*/
public static void lcs(int i,int j, int[]x,int [][]b)
{
if(i==0 || j == 0) return;
if(b[i][j] == 1)
{
//即第二种情况,X和Y最后一个元素相同
lcs(i-1,j-1,x,b); //递归调用
System.out.print(x[i-1]);
}
else if(b[i][j] == 2)
{
//即第三种情况中的第一种情况,右侧大于左侧
lcs(i-1,j,x,b);
}
else
{
//即第三种情况中的第二种情况,左侧大于右侧
lcs(i,j-1,x,b);
}
}
/**
* P58页,最长公共子序列代码
* @param x 序列X
* @param y 序列Y
* @param b 状态字,用于判断序列满足哪种情况
* @return 返回X和Y的最长公共子序列长度
*/
public static int lcsLength(int[]x,int[]y,int [][]b)
{
int m = x.length;
int n = y.length;
int [][]c = new int[m+1][n+1];
//初始化边界条件
for(int i=0;i<=m;i++)
c[i][0] = 0;
for(int i=0;i<=n;i++)
c[0][i] = 0;
for(int i=1;i<=m;i++)
{
for(int j=1;j<=n;j++)
{
if(x[i-1] == y[j-1])
{
//第二种情况,即此部分X和Y最后一个元素相同,那么最长公共子序列长度为之前的序列的最长公共子序列的长度+1
c[i][j] = c[i-1][j-1] + 1;
b[i][j] = 1;
}
else if(c[i-1][j] >= c[i][j-1])
{
//第三种情况中的第一种,即右侧的最长公共子序列的长度大于左侧,那么X和Y的最长公共子序列长度即为右侧
c[i][j] = c[i-1][j];
b[i][j] = 2;
}
else
{
//第三种情况中的第二种,即左侧的最长公共子序列的长度大于右侧,那么X和Y的最长公共子序列长度即为左侧
c[i][j] = c[i][j-1];
b[i][j] = 3;
}
}
}
return c[m][n];
}
public static void main(String[] args) {
//char []X = {' ','A','B','E','B','D','A','B'};
//char []Y = {'B','D','C','A','B','A'};
//char []X = {'C','B','A'};
//char []Y = new char[X.length];
int []X = {5,2,3,4,8,6,9};
int []Y = new int[X.length];
for(int i=0;i<Y.length;i++)
Y[i]=X[i];
Y = Sort(Y);
int [][]b = new int[X.length+1][Y.length+1];
int x = lcsLength(X,Y,b);
System.out.println(x);
lcs(X.length,Y.length,X,b);
x+=1;
}